최대공약수 이야기

최대공약수와 친해지기

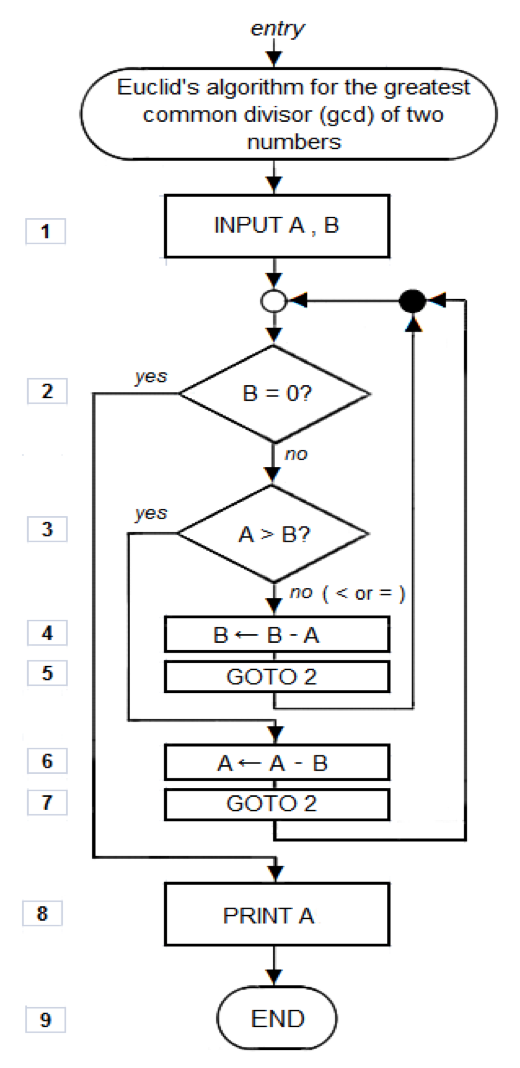
최대공약수
(Great Common Divisor)

최대공약수(最大公約數)란, 0이 아닌 두 정수나 다항식의 공통되는 약수 중에서 가장 큰 수를 말한다. 두 정수 a와 b의 최대공약수를 기호로 gcd(a, b)로 표기하거나, 더 간단히 (a, b)로도 표기한다.

최대공약수의 특징

1. gcd(a, b)는 a와 b의 약수이다.
2. 두 수 또는 다항식의 곱은 두 수의 최대공약수와 최소공배수의 곱과 같다.
  gcd(a, b)·lcm(a, b) = a·b
3. a와 b의 최대공약수 gcd(a, b)의 값은 ax + by 꼴의 수(x, y는 정수) 중 가장 작은 양수의 값과 같다.
4. 만약 두 정수의 최대공약수가 1과 -1밖에 없는 경우, 이 두 수는 서로소라고 부른다.
5. 만약 두 다항식의 상수 이외의 최대공약수가 없을 경우, 이 두 다항식은 서로소라고 부른다.

유클리드 알고리즘

유클리드와 알고리즘의 소개

유클리드(고대 수학자)

자바스크립트 계산기

두개의 숫자를 입력해보세요.